Guitar chord theory can initially seem daunting, and many guitarists, especially beginners, might shy away from delving into it. It’s common to focus on learning chords practically – shapes and fingerings – without grasping the underlying structure that governs them. Like many, in my early guitar journey, I prioritized lead guitar techniques, inspired by legends, and neglected the foundational aspects of chords and rhythm. However, dedicating time to understanding guitar chord structure and theory has profoundly transformed my playing.
Developing a strong grasp of chord structure has not only broadened my chord vocabulary and confidence across the fretboard but has also significantly enhanced my lead guitar playing. This might seem counterintuitive if your primary interest is soloing. However, chords are the harmonic bedrock upon which melodies and solos are built.
When you improvise or compose a guitar solo, you are essentially weaving musical lines over a chord progression. Understanding how chords are constructed and their function within a musical context allows you to create solos that are not just technically proficient but also harmonically richer and more integrated with the underlying music. It enables you to play with the music, rather than just over it, resulting in more melodic, impactful, and sophisticated solos.
Furthermore, if you aspire to write your own music, a solid understanding of guitar chord structure is indispensable. It empowers you to create compelling and nuanced chord progressions that effectively convey the mood and style you aim for in your compositions.
Guitar chord theory is extensive, encompassing a wide range of concepts that cannot be fully covered in a single article. Therefore, this guide will focus on the fundamentals – the essential building blocks of guitar chord structure. We will explore the basics to provide you with a foundational understanding of how chords are formed. This knowledge will make learning new chords and applying them in your playing significantly more intuitive and efficient. As you progress, you can build upon this foundation to deepen your theoretical knowledge and practical application.
In this article, we will explore:
It’s important to note that this article is designed to build theoretical understanding, not to be a collection of chord diagrams. Practical chord shapes will be explored in future resources. The aim here is to equip you with the theoretical knowledge that underpins chord construction, making your journey of learning and using chords on the guitar more informed and effective. Whether you want to improve your rhythm guitar skills, write original music, or simply become a more well-rounded musician, understanding chord structure is a critical step. Let’s begin with the foundation: the major scale.
The Foundational Major Scale in Chord Structure
To truly grasp guitar chord theory and the creation of guitar chords, we must begin with the major scale. While it might not immediately appear relevant, the major scale is the cornerstone of Western music harmony, including blues, rock, pop, and countless other genres. It serves as the fundamental source from which chords are derived and understood.
If you are new to the major scale, it would be beneficial to first familiarize yourself with its patterns and sounds. The major scale is a seven-note scale characterized by a specific intervallic formula. Every scale in music is defined by its unique formula, and for the major scale, this formula is:
| Degree | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|
Each number in this formula represents a degree within the major scale. ‘1’ is the root note, ‘2’ is the second note, and so forth, up to the ‘7th’ degree. In the key of C major, for instance, the notes of the major scale are:
| Degree | 1st (Root) | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| Note | C | D | E | F | G | A | B |
Visually, on the guitar fretboard, the C major scale can be played across the neck like this:
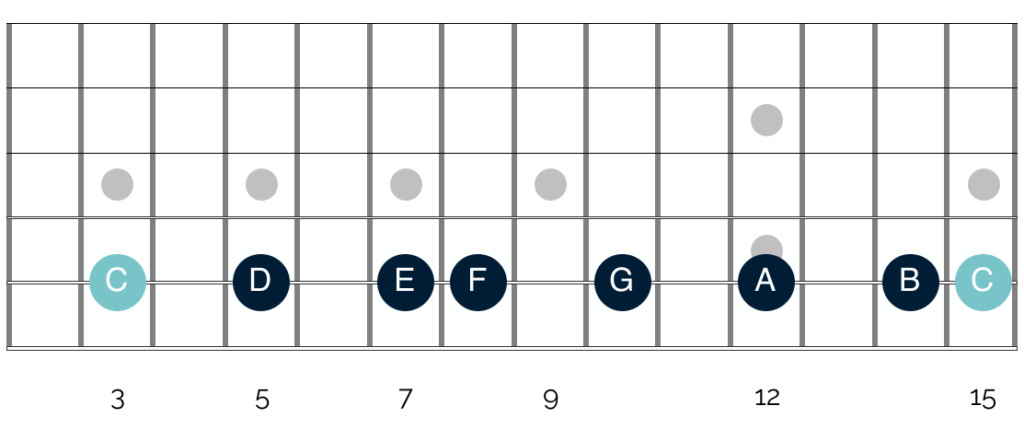Understanding the major scale is the first step to understanding guitar chord theory
In music theory, a chord is defined as a combination of at least three notes played simultaneously, creating harmony. To construct a chord from the major scale, we need to select and ‘stack’ at least three notes from it. However, chord construction isn’t arbitrary. There is a logical system that dictates which notes are combined and how they relate to each other. Understanding this logic is crucial. While it might seem complex initially, grasping this system will significantly simplify learning and utilizing chords effectively in your guitar playing.
Building Triads: The Simplest Chord Structure
The specific notes chosen from the major scale, the number of notes combined, and their arrangement determine the type of chord created. These factors allow for a wide variety of chords, each with a unique sonic character. Let’s start with the simplest form of chord construction: triads.
In music theory, a triad is the most basic type of chord, consisting of just three notes. As the name suggests (“tri-“), it’s a chord built upon three tones. Specifically, a triad is formed by stacking three notes, each separated by an interval of a third. The term “third” refers to a musical interval.
If you are unfamiliar with intervals or need a refresher, understanding musical intervals is crucial for chord theory. Intervals define the distance in pitch between two notes and are fundamental to understanding harmony.
Let’s revisit the C major scale as an example:
| Note Name | C | D | E | F | G | A | B |
|---|---|---|---|---|---|---|---|
| Scale Degree | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
The notes highlighted in yellow (C, E, and G) in the table above constitute a C major triad. As mentioned, a triad consists of three notes, each separated by a ‘third’. The terminology of “third” can be initially confusing. You might notice that between C and E, there’s only one intervening note (D), and similarly, between E and G (F). It seems like a “second” rather than a “third”.
However, in musical interval counting, we always include the starting note. So, counting from C in the major scale: C is one, D is two, and E is three. Thus, E is a third from C. Similarly, from E: E is one, F is two, and G is three. G is a third from E.
Another way to think about this is to skip every other note in the scale. Start on C, skip D, play E, skip F, play G, and so on. This ‘skip-note’ method helps visualize the notes of a triad.
To form a triad, you simply select three notes from the major scale, each a third apart. Playing these notes simultaneously creates a triad.
Intervals Within Triads: Major and Minor Qualities
Now, the character of a triad becomes more nuanced when we consider the specific intervals between its notes. The starting note of a triad within the major scale significantly affects its quality, meaning whether it’s major, minor, or something else.
In our C major scale example, starting on C and building a triad resulted in a C major triad. However, this isn’t the case if we start on a different note of the scale. This variation arises because of the intervals between the notes within the scale itself. While a triad is always constructed with notes a ‘third’ apart in scale degrees, the actual musical interval (the distance in pitch) between these notes can differ, leading to different triad types.
If you are familiar with the major scale, you know that the distances – or intervals – between consecutive notes aren’t uniform. This is evident when you visualize the scale on the guitar fretboard:
Understanding the major scale is the first step to understanding guitar chord theory
Notice that some notes are separated by two frets (a whole step), while others are only one fret apart (a half step). These varying intervals within the major scale are crucial when constructing triads from different starting points.
Even though each triad is built by stacking notes a third apart in scale degrees, the precise intervals between these notes change depending on the starting note, resulting in different triad qualities. Let’s compare a triad built starting on C with one starting on D in the C major scale.
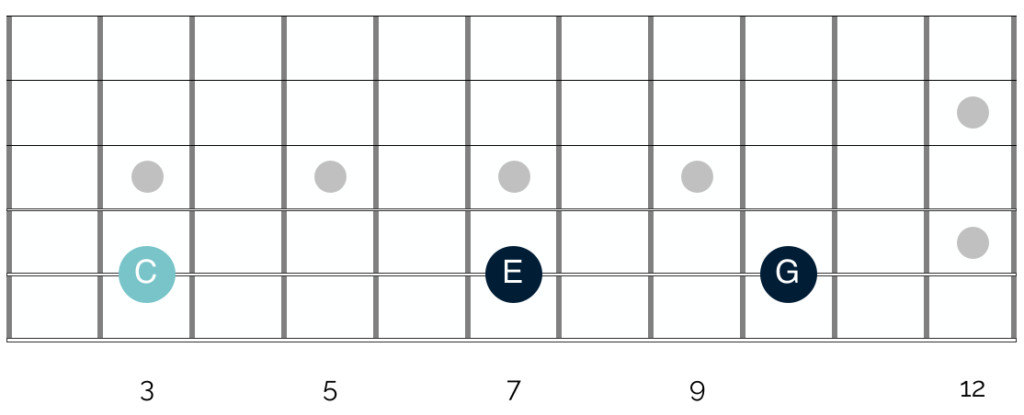C Major Triad Intervals
In the first diagram, the root note of the triad is C (in light blue). The interval between C and E spans four frets on the guitar. The interval between E and G spans three frets. From C to G, the total span is seven frets.
Each fret on a guitar represents a semitone, or half step. Therefore, four frets equal two whole tones (whole steps), and three frets equal one and a half tones (a minor third interval). Seven frets equal three and a half tones (a perfect fifth interval).
Now, let’s examine a triad built starting on D in the C major scale:
D Minor Triad Intervals
Comparing this to the triad built on C, the intervals are different. Between D and F, there are only three frets (one and a half tones). However, between F and A, there are four frets (two tones). Like the C triad, the distance from the root (D) to the highest note (A) is seven frets, or three and a half tones.
If you play the notes of the C triad (C, E, G) and the D triad (D, F, A) simultaneously, you’ll hear a distinct difference. The C triad sounds like a C major triad, while the D triad sounds like a D minor triad.
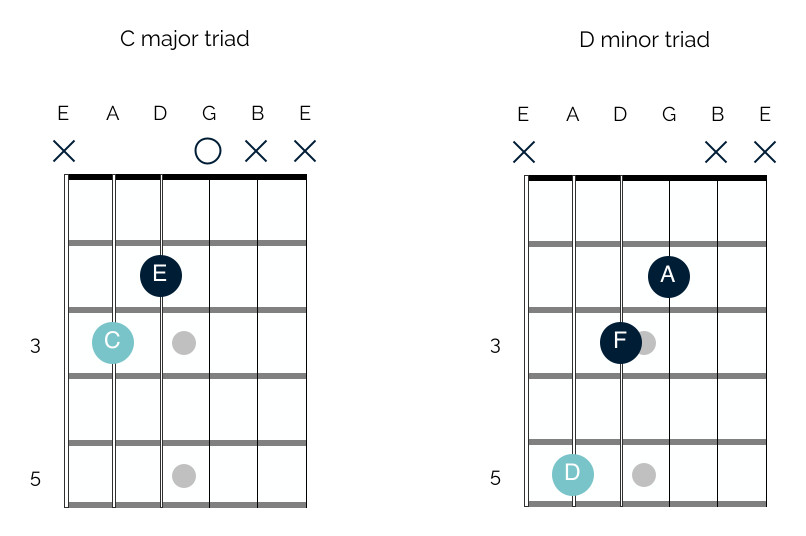C Major and D Minor Triads
The C major triad example here uses open strings for simplicity, showing the G note on the open G string rather than fretted.
Play both these triads and listen carefully to their sounds. Major triads typically have a bright, uplifting, or “happy” quality. Minor triads, conversely, have a darker, somber, or “sad” quality. These contrasting emotional characteristics are fundamental to the use of major and minor chords in music.
The difference in sound between major and minor triads arises from the specific intervals between their notes. This concept of intervals is central to guitar chord theory and is explored in more detail below.
Major and Minor Triads: Defining Intervals
As we’ve seen, constructing a triad starting on C in the key of C major results in a C major triad, whereas starting on D produces a D minor triad. Let’s examine the intervals that define these qualities more closely.
Looking again at the fretboard visualization of a C major triad:
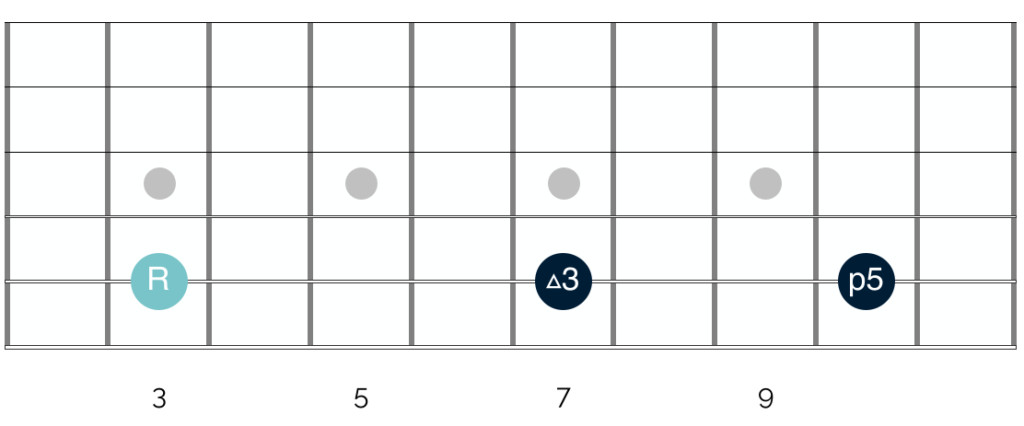C Major Triad Intervals Defined
This diagram highlights the intervals within the C major triad:
- Root: C (the starting note, defining the chord name).
- Major Third: The interval from the root to the second note (C to E). A major third is always four frets or two whole tones above the root. This interval is what gives the major triad its characteristically bright sound.
- Perfect Fifth: The interval from the root to the third note (C to G). A perfect fifth is always seven frets or three and a half tones above the root. Perfect intervals are considered very consonant and stable in music. The perfect fifth contributes to the overall stable and harmonious sound of the major triad, lacking dissonance or tension.
Now, let’s compare these intervals to those in a D minor triad:
D Minor Triad Intervals Defined
Here are the intervals within the D minor triad:
- Root: D.
- Minor Third: The interval from the root to the second note (D to F). A minor third is always three frets or one and a half tones above the root – one fret (a half step) smaller than a major third. This minor third interval is what imparts the minor triad’s melancholic quality.
- Perfect Fifth: The interval from the root to the third note (D to A). Like the major triad, the minor triad also contains a perfect fifth above the root. This shared perfect fifth means that while minor triads have a darker sound, they also retain a sense of stability and resolution, similar to major triads, and are not inherently dissonant.
The key distinction between major and minor triads lies solely in the third interval – major triads have a major third, and minor triads have a minor third. The perfect fifth is common to both, contributing to their triad stability, despite their contrasting emotional qualities.
Harmonizing the Major Scale: Triad Types on Each Degree
To further understand guitar chord theory, we need to apply the concept of triad construction to every note of the major scale. This process, known as harmonizing the major scale, reveals the pattern of triad types that naturally occur within a major key.
Let’s return to the notes and degrees of the C major scale:
| Note Name | C | D | E | F | G | A | B |
|---|---|---|---|---|---|---|---|
| Scale Degree | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
Starting with C (the 1st degree), construct a triad by selecting every other note: C, E, and G. Then, repeat this process starting on D (the 2nd degree), then E (3rd), and so on, for all seven notes of the scale. When you reach the 7th degree (B), continue ‘skipping’ notes, wrapping around to the beginning of the scale if necessary to complete the triad. For example, starting on F, the triad notes are F, A, and C. For G, they are G, B, and D.
As you perform this exercise for each degree of the major scale, keep in mind the intervals that define major and minor triads:
- Major Triad: Contains a root, a major third (4 frets/2 whole tones above the root), and a perfect fifth (7 frets/3.5 whole tones above the root).
- Minor Triad: Contains a root, a minor third (3 frets/1.5 whole tones above the root), and a perfect fifth (7 frets/3.5 whole tones above the root).
Upon harmonizing the entire major scale, you will discover two significant patterns. First, the process yields a mix of both major and minor triads. Second, the triad built on the 7th degree of the scale has a different quality from both major and minor triads – it’s a diminished triad.
Here’s the result of harmonizing the C major scale:
| Scale Degree | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| Notes in Triad | C-E-G | D-F-A | E-G-B | F-A-C | G-B-D | A-C-E | B-D-F |
| Triad Type | Major | Minor | Minor | Major | Major | Minor | Diminished |
Notice the pattern: Major, Minor, Minor, Major, Major, Minor, Diminished. This sequence of triad types is consistent across all major scales, regardless of the key. Whether in A major, B major, D major, or any other major key, harmonizing the scale degrees will always produce this same sequence of major, minor, and diminished triads. The specific notes will change depending on the key, but the order of triad qualities remains constant.
This pattern is fundamental because musicians use these sequences of chords to create chord progressions. The consistent nature of this pattern in all major keys is a cornerstone of harmonic structure in Western music. We will explore chord progressions in more detail later. First, let’s examine the diminished triad, which emerges from harmonizing the 7th degree of the major scale, and understand what makes it unique.
Diminished Triads: The Exception in the Major Scale
As you may have noticed when harmonizing the major scale, the triad built on the 7th scale degree stands apart. It’s neither major nor minor; it’s a diminished triad. Let’s investigate the intervals within this triad to understand its unique character.
Consider the B diminished triad (from the C major scale), composed of the notes B, D, and F. Visually on the guitar fretboard, these notes are:
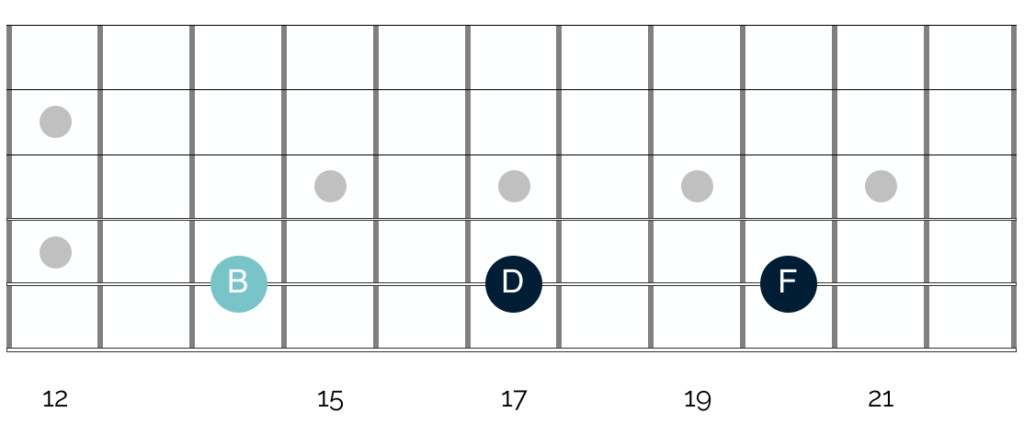Diminished Triad Notes
The formation of this triad appears similar to major and minor triads – it’s still built by stacking notes a third apart in scale degrees. So, why is it diminished and not simply major or minor? The answer lies in the intervals between these notes.
Let’s analyze the intervals of the B diminished triad:
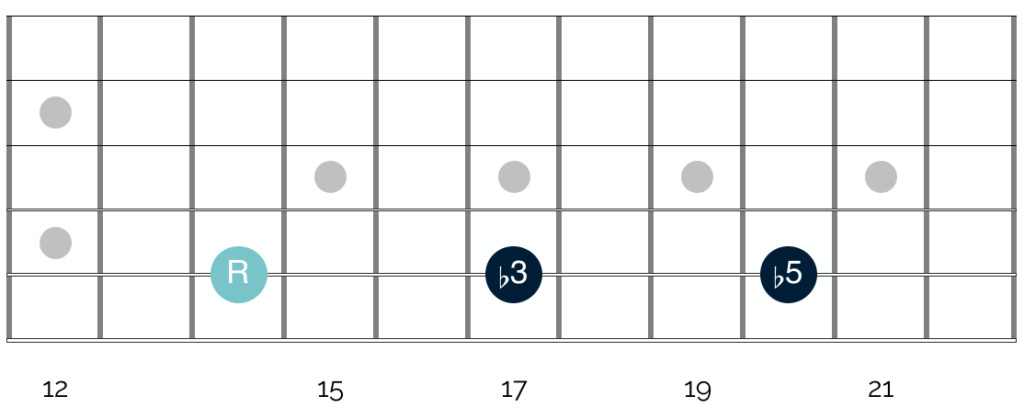Diminished Triad Intervals Defined
The intervals are:
- Root: B.
- Minor Third: The interval from the root to the second note (B to D). This is a minor third, consistent with minor triads – three frets or 1.5 tones above the root.
- Diminished Fifth (or “Flat Fifth”): The interval from the root to the third note (B to F). This is where the diminished triad differs significantly. Instead of a perfect fifth (7 frets), it’s a diminished fifth, also known as a “flat fifth” – only six frets or 3 whole tones above the root.
The diminished fifth is the defining interval of a diminished triad. Unlike the consonant and stable sound of a perfect fifth, the diminished fifth is dissonant, creating a tense and unresolved quality. This dissonance is what gives diminished chords their unique, often described as unstable or even unsettling, sound.
Due to their inherent tension, diminished triads and chords are used less frequently than major and minor chords. However, they are far from unimportant. Diminished chords play crucial roles in creating harmonic interest, adding tension and release in chord progressions, and providing pathways for modulation to different keys. While you might not use them as often as major or minor chords, understanding and utilizing diminished chords is essential for a comprehensive grasp of guitar chord theory and harmony.
Triads and Chords: Practical Application on Guitar
At this point, you might be wondering how to apply this theoretical knowledge of triads practically to your guitar playing. Understanding triads and their construction is valuable, but bridging the gap to actual guitar chords is essential for practical application.
So far, we have discussed triads in their theoretical, purest form – three notes, each a third apart, defining a chord quality. In the context of guitar chord theory, this is a crucial foundational step. However, the term “triad” is more commonly used in music theory discussions, while guitarists more frequently use the term “chord.”
To connect these concepts, it’s important to clarify the relationship between triads and chords in a practical guitar context. A triad, by definition, is a three-note chord. Therefore, all triads are chords. However, not all chords are triads. Many common guitar chords are built upon triads but may include additional notes or doubled notes for a fuller sound or specific voicing.
In practice, you are not limited to playing only three strings or frets when playing a chord. Guitar chords often involve playing across all six strings, or a subset of strings, to create richer harmonic textures.
Let’s revisit the C major triad we discussed earlier, shown in its most basic three-note form:
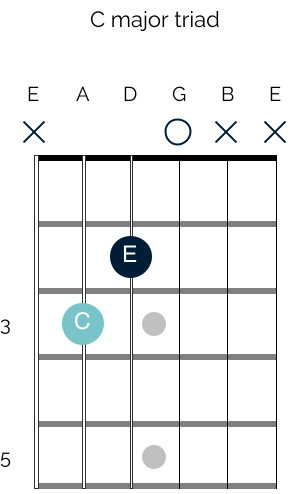Basic C Major Triad
This diagram shows a triad with only three notes. If you are new to chord theory, this specific triad shape might not be one you frequently use in your playing.
However, you are likely very familiar with this common C major chord shape:
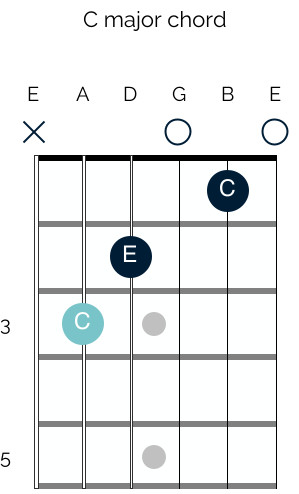Standard C Major Chord
This diagram shows the notes in a standard open-position C major chord. While we call the first diagram a C major triad and the second a C major chord, the terms are often used interchangeably because they are fundamentally the same chord. Both contain the same core notes: C, E, and G.
The C major triad (the three-note version) contains the notes C, E, and G. The standard open C major chord, when played, also consists of the notes C, E, and G, but with some notes repeated. In the open C chord, you are playing C, E, G, C, and E.
It’s still considered a C major triad because it is built upon and contains only the three unique notes C, E, and G. The repetition of notes doesn’t change the fundamental triad structure. This principle applies to most basic major and minor chords you’re likely to learn as a guitarist.
Consider the G major chord. A G major triad consists of the notes G, B, and D. A pure G major triad can be played on the guitar like this:
G Major Triad Shape
Here, the triad is played across the 6th, 5th, and 4th strings, with the open D string providing the D note.
However, when you play a full G major chord, you typically strum all six strings. As you can see in the diagram, even in the full six-string G major chord, the notes are still drawn from the G major triad: G, B, and D. You play open G and B strings, and then a G note on the high E string. The other notes in the full chord are also repetitions or octaves of G, B, or D.
Understanding that common guitar chords are often built upon triads helps bridge the theory to practice. It shows that the triads we’ve discussed are not just abstract theoretical constructs but are the very foundation of the chords you play every day.
Creating Chord Progressions with Triads
Recognizing that triads form the basis of familiar major and minor chords is a crucial step. It connects the theoretical concepts to chords you’ve likely been playing since you began guitar. With this understanding, we can now explore how to combine these chords to create chord progressions – the sequence of chords that form the harmonic structure of music.
Let’s revisit the table that summarized the triad types derived from harmonizing the major scale:
| Scale Degree | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|————–|—–|—–|—–|—–|—–|—–|—–|—–|
| Notes in Triad | C-E-G | D-F-A | E-G-B | F-A-C | G-B-D | A-C-E | B-D-F |
| Triad Type | Major | Minor | Minor | Major | Major | Minor | Diminished |
| Chord Name | C Major | D Minor | E Minor | F Major | G Major | A Minor | B Diminished |
| Triad Number | I | ii | iii | IV | V | vi | vii°|
In this table, we’ve added rows for “Chord Name” and “Triad Number.” The “Triad Number” row uses Roman numerals to represent each triad’s position in the scale. This numbering system is analogous to scale degrees but applied to chords. Uppercase Roman numerals (I, IV, V) denote major triads, and lowercase numerals (ii, iii, vi, vii) denote minor and diminished triads. The diminished triad is indicated by a lowercase Roman numeral with a small circle (vii°).
Musicians use these chords, in this specific order of qualities (major, minor, etc.), to create chord progressions within a major key. Songs written in the key of C major, for example, will typically draw their chords primarily from this set of seven chords derived from the C major scale.
A well-known example is “Let It Be” by The Beatles, which is in the key of C major. The verse chord progression includes: C major, G major, A minor, F major. In Roman numeral notation, this is I, V, vi, IV.
Guitarists and musicians often discuss chord progressions using these Roman numerals. If you’ve heard musicians refer to a “1-4-5” progression, they are using this Roman numeral system. They are simply describing the type of chord (major, minor, etc.) and its position in the key.
For instance, if you are in a jam session and someone says, “Let’s play a I-IV-V in the key of C,” you immediately know the chord progression: C major (I), F major (IV), and G major (V). This system provides a universal language for describing and understanding chord progressions across all major keys.
Beyond Basic Guitar Chord Theory: Extensions and Complexity
Chord progressions are not always as straightforward as using only the basic triads derived from a single major scale. There are nuances and complexities that expand beyond these foundational concepts. Two main factors contribute to this complexity:
Firstly, musicians often venture beyond the chords strictly within one major scale. While a song might be primarily in a major key and use chords from that scale, songwriters frequently incorporate key changes or “borrow” chords from other keys or modes. This borrowing adds harmonic color and interest to progressions.
Therefore, while understanding the chords harmonized from the major scale is a significant step in guitar chord theory, it’s just the beginning. To fully analyze and understand the harmonic richness of diverse musical styles, further theoretical knowledge is needed. These advanced concepts are beyond the scope of this introductory article but will be explored in future discussions. For now, it’s important to recognize that chord progressions can be more varied and colorful than simple progressions within a single major scale.
Secondly, guitarists and musicians often embellish basic triads by adding “chord extensions.” Chord extensions are notes added to a basic triad that are beyond the root, third, and fifth. Common extensions include the 7th, 9th, 11th, and 13th. These extensions don’t fundamentally alter whether a chord is major or minor, but they significantly change its sound and feel, adding layers of harmonic complexity and sophistication.
Chord extensions are prevalent in virtually all genres of popular music. You’ve undoubtedly encountered them in forms like major 7th chords, minor 7th chords, and dominant 7th chords. Like advanced chord progressions, chord extensions are a more in-depth topic requiring dedicated explanation.
However, the good news is that a solid grasp of the basic guitar chord theory outlined in this article – understanding triads and their construction – makes understanding chord extensions much easier. Chord extensions are built upon the foundational triad structure.
For now, focus on mastering the fundamental guitar chord theory presented here. This material is dense and theoretical, so it’s perfectly normal if it feels challenging or confusing at first. The key is to revisit these concepts, apply them to your guitar, and practice identifying triads and their qualities. With time and consistent effort, these concepts will become clearer and more intuitive, significantly enhancing your musical understanding and guitar playing.
Good luck on your journey into guitar chord theory! If you have any questions or want to share your progress, please reach out. Leave a comment below or send an email. I’m here to help!
References & Images
Unsplash, Guitar Habits, Wikipedia, Hello Music Theory, Music Notes Now, Wikipedia, Puget Sound, Open Music Theory, Guitar Theory For Dummies, Modern Music Theory For Guitarists
