The circle of fifths can seem like a mysterious concept, especially for guitar players who haven’t delved deep into music theory or genres like jazz and classical. You might have heard conflicting opinions, some hailing it as an essential practice tool, while others dismiss it as a theoretical abstraction with little practical value for guitarists.
My first encounter with the circle of fifths was in a high school music theory class. Back then, it felt like just another academic hurdle, something to memorize for tests. Beyond recognizing key signatures on sheet music, its real-world application to playing guitar remained elusive.
Years later, as I started to pinpoint the gaps in my musical understanding, the circle of fifths resurfaced as a crucial element.
The circle of fifths is, in fact, an invaluable asset for guitarists aiming to master scales and arpeggios across the entire fretboard. Instead of confining your practice to a single key, using the circle encourages you to transpose musical ideas through all 12 keys. This systematic approach dramatically improves your fretboard knowledge and internalizes the nuances of all 12 diatonic keys.
The linear layout of the guitar fretboard makes it deceptively simple to learn a scale or arpeggio shape and then just slide that same shape up and down the neck to transpose it. Shift an A major scale up one fret, and instantly it transforms into a Bb major scale.
However, practicing with the circle of fifths elevates your musical proficiency to a new level. Think of it as adding resistance to your musical workout. Instead of simply moving a scale pattern up a fret, challenge yourself by transposing it up a perfect fifth or down a perfect fourth. Continue this cyclical movement until you’ve explored the pattern in every key.
This method will unlock the guitar fretboard in ways you may not have thought possible, expanding your musical horizons and dexterity.
Understanding How the Circle of Fifths Works
The circle of fifths is visually represented as a circle divided into 12 equal segments. Each segment corresponds to one of the 12 notes within the chromatic scale. Moving clockwise around the circle, each note ascends by a perfect fifth interval. Conversely, moving counterclockwise results in a descent by a perfect fourth.
However, the circle’s true power isn’t just in memorizing note order. Simply reciting the 12 chromatic notes won’t make you a musical virtuoso, just as knowing the alphabet doesn’t automatically make you a bestselling author.
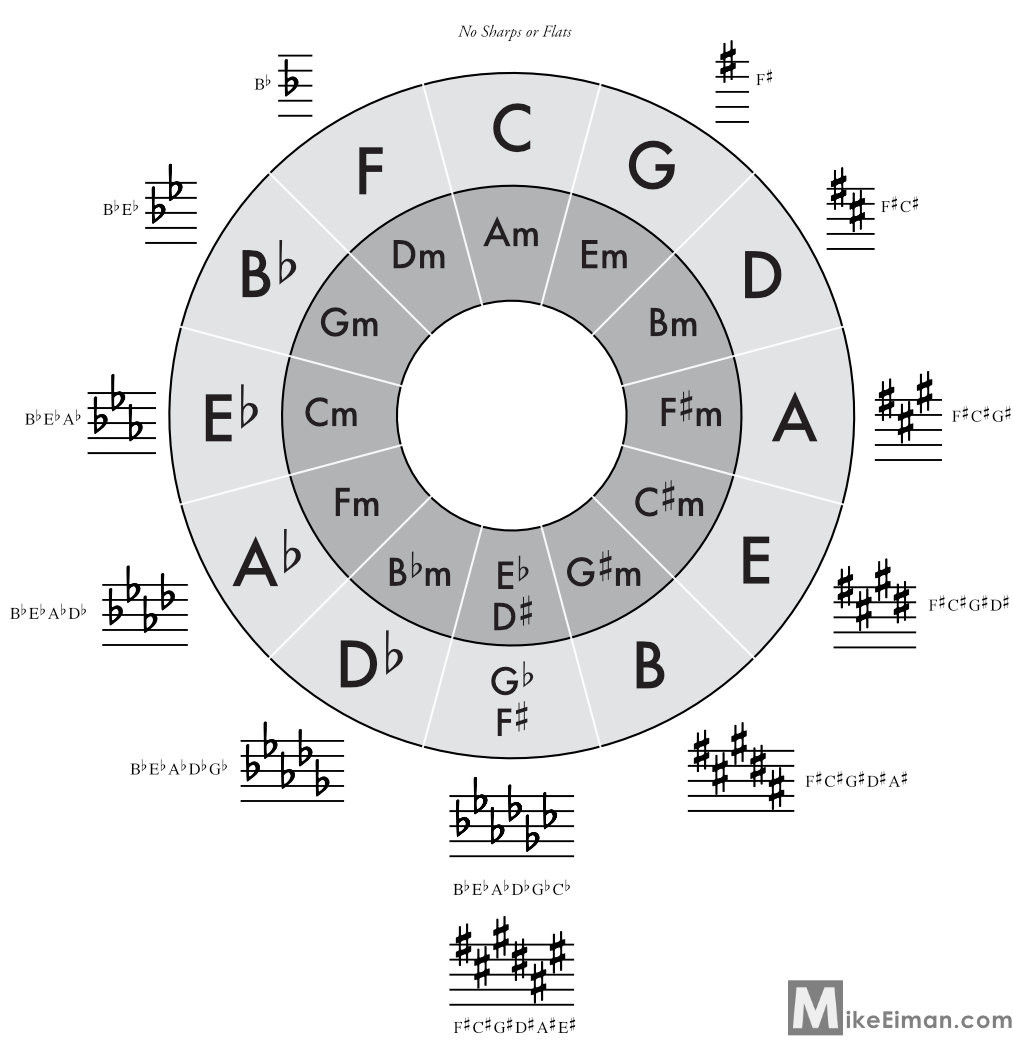
A complete circle of fifths diagram showing major keys on the outer ring and their relative minor keys on the inner ring, essential for understanding key relationships in music theory.
The circle of fifths is most effectively used to teach and understand the order of sharps and flats in musical key signatures. This knowledge is fundamental for determining which notes are naturally included in a particular key.
C major, the starting point, is devoid of sharps or flats. But unless you intend to confine your playing to C major exclusively, understanding sharps and flats is crucial. If you’re serious about developing a comprehensive understanding of musical language, recognizing key signatures in written music becomes essential.
Fortunately, there are memorable mnemonics to help you learn the order of sharps and flats:
- Order of Sharps: Fat Cats Go Down Alleys Eating Birds (F#, C#, G#, D#, A#, E#, B#)
- Order of Flats: Before Eating A Donut, Get Coffee First (Bb, Eb, Ab, Db, Gb, Cb, Fb)
While these memory aids are helpful for recalling the sequence of sharps and flats, they don’t inherently tell you how many sharps or flats are in a specific key. They help you remember the order, but not the quantity per key.
Ultimately, there’s no substitute for learning the key signatures directly – knowing, for instance, that D major has two sharps and Db major has five flats. However, there are practical shortcuts to quickly identify key signatures once you grasp the underlying principles.
Decoding Flat Keys
In most commonly encountered music, you’ll primarily deal with six flat keys. Interestingly, one of these doesn’t explicitly include “flat” in its name.
The key with a single flat is F major. It deviates slightly from the naming pattern of other flat keys, so memorizing it is necessary.
For all subsequent flat keys (those with two or more flats), the key name is derived from the second-to-last flat in the key signature’s sequence. For example, the key signature with four flats (Bb, Eb, Ab, Db) represents the key of Ab major. The second to last flat is Ab, which gives the key its name.
It requires some practice to become fluent. The common mistake is to read through all the flats and try to name the key based on the very last flat. Instead, you must always focus on the second-to-last flat in the series.
This table clarifies the relationship between flat keys and their key signatures:
| Key | Bb | Eb | Ab | Db | Gb | Cb | Fb |
|---|---|---|---|---|---|---|---|
| F Major | X | ||||||
| Bb Major | X | X | |||||
| Eb Major | X | X | X | ||||
| Ab Major | X | X | X | X | |||
| Db Major | X | X | X | X | X | ||
| Gb Major | X | X | X | X | X | X |
Why does this table stop at Gb major? Because keys like Cb major or Fb major are exceptionally rare. You might already understand the reason.
The note a half-step below C is generally B. Sometimes, the same musical pitch can have different names – this is known as enharmonic equivalence. Cb (C flat) is enharmonically equivalent to B. Since we already have B major (with five sharps), B major is almost always preferred because it is simpler to read and write in musical notation.
Similarly, the note a half-step below F is E. Fb major is enharmonically equivalent to E major (which uses four sharps). Again, E major is the more practical and common choice.
Navigating Sharp Keys
If flat keys seemed a bit tricky, the good news is that sharp keys follow a slightly more consistent pattern, making them arguably easier to grasp. The method for identifying a sharp key signature is uniform across all sharp keys.
The last sharp added in a sharp key signature is always a half-step below the root note (tonic) of the major key. For instance, the key signature with one sharp (F#) indicates G major. With four sharps (F#, C#, G#, D#), the key is E major. D# being a half step below E.
The table below illustrates the sharps present in each sharp key:
| Key | F# | C# | G# | D# | A# | E# | B# |
|---|---|---|---|---|---|---|---|
| G Major | X | ||||||
| D Major | X | X | |||||
| A Major | X | X | X | ||||
| E Major | X | X | X | X | |||
| B Major | X | X | X | X | X | ||
| F# Major | X | X | X | X | X | X |
Unlike flat keys, where enharmonic equivalents are seldom used, you might occasionally encounter music written in F# major. As you might suspect, F# major is enharmonically equivalent to Gb major. Its key signature includes E#, which is, in turn, enharmonically equivalent to F.
The key of C# major also introduces B# into its signature. While “B Sharps” might sound like a quirky name for a barbershop quartet (a nod to The Simpsons!), using seven sharps becomes unnecessarily complex when four flats can express the same tonality more efficiently.
Fortunately, most composers tend to avoid F# major and C# major, opting for their enharmonic flat key counterparts for simplicity.
Discovering Minor Keys
You can easily find the relative minor key for any major key by descending a minor third from the major key’s root note. For example, to find the relative minor of Bb major, count down a minor third: Bb -> A -> G. Therefore, G minor is the relative minor of Bb major.
If you want to identify a minor key directly from its key signature, descending a minor third from the major key is the most straightforward method. However, there are alternative shortcuts, particularly different approaches for sharp and flat key signatures.
For flat key signatures, count up a major third from the last flat in the key signature. For instance, in Ab major, the last flat is Db. Counting up a major third from Db: Db -> Eb -> F. Thus, F minor is the relative minor of Ab major.
This technique even applies to F major, which has Bb as its single flat. Counting up a major third from Bb: Bb -> C -> D, revealing D minor as the relative minor of F major.
Once again, sharp key signatures offer a slightly simpler method. Take the last sharp in the key signature and descend a whole step. In G major, the last sharp is F#. A whole step below F# is E. Consequently, E minor is the relative minor of G major.
Sharps and Flats: A Quick Reference
The most effective way to truly learn the circle of fifths is to actively engage with it. Start practicing scales on a single guitar string, systematically progressing through the circle of fifths. Extend this practice to multiple strings. Practice both major and minor arpeggios, following the circle of fifths progression. The key is to be creative and apply it practically to your guitar playing.
The more you practice in all 12 keys, the more deeply you’ll internalize the characteristic notes of each key. Over time, you’ll notice a significant improvement in your improvisational skills, hitting fewer “wrong” notes during solos and developing a more intuitive understanding of harmony.
If you’re still finding it challenging to visualize how sharps and flats integrate into each diatonic key, the following reference chart can be a valuable tool:
| Root | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| C | D | E | F | G | A | B |
| G | A | B | C | D | E | F# |
| D | E | F# | G | A | B | C# |
| A | B | C# | D | E | F# | G# |
| E | F# | G# | A | B | C# | D# |
| B | C# | D# | E | F# | G# | A# |
| Gb | Ab | Bb | Cb | Db | Eb | F |
| Db | Eb | F | Gb | Ab | Bb | C |
| Ab | Bb | C | Db | Eb | F | G |
| Eb | F | G | Ab | Bb | C | D |
| Bb | C | D | Eb | F | G | A |
| F | G | A | Bb | C | D | E |
