When analyzing the sound of an acoustic guitar using a spectrogram, one might expect to see a clear, dominant peak at the fundamental frequency of the played note, followed by progressively weaker harmonics at integer multiples of this fundamental. However, real-world spectrograms often reveal a more complex picture, where the fundamental frequency appears “washed out” or broadened into the background, challenging the idealized models of string vibration taught in basic physics. This phenomenon is particularly noticeable in the lower frequencies of the Spectrum Acoustic Guitar.
The initial observation of a less-than-ideal fundamental peak in the spectrum acoustic guitar raises questions about why the sound deviates from a simple harmonic series. Several factors contribute to this deviation, moving beyond the simplistic view of a guitar string as a perfect, isolated oscillator. These factors are deeply intertwined with the physics of string vibration, the instrument’s construction, and even the player’s technique.
One crucial aspect is that real guitar strings are not perfectly ideal strings. Elementary physics often models strings as perfectly flexible, uniform, and under ideal tension. In reality, guitar strings possess complex material properties, and their behavior is not purely linear. Factors like string composition, tension, and even the way a string is plucked (position, force, angle) all influence the resulting spectrum acoustic guitar. Furthermore, the interaction of the vibrating string with the guitar body and other strings introduces significant complexity.
The guitar body acts as a resonant chamber, amplifying certain frequencies and dampening others, shaping the overall timbre of the instrument. Similarly, the other strings on the guitar, even when not actively played, can resonate sympathetically with the vibrating string, further enriching the sound and influencing the spectrum acoustic guitar. This interplay of resonances leads to a more complex frequency distribution than a single, isolated string would produce.
The broadening of the peaks, particularly at lower frequencies in the spectrum acoustic guitar, is related to a phenomenon called dispersion. In an ideal string, all harmonics would be perfectly sharp peaks, represented mathematically as delta functions. However, the non-linearities and complexities of real strings introduce dispersion, meaning that the speed of waves traveling along the string is not constant across all frequencies. This frequency-dependent wave speed causes the harmonic peaks to broaden, effectively spreading their energy across a wider range of frequencies. This effect appears to be more pronounced at lower frequencies, contributing to the “washed out” appearance of the fundamental in the spectrum acoustic guitar’s lower end.
[
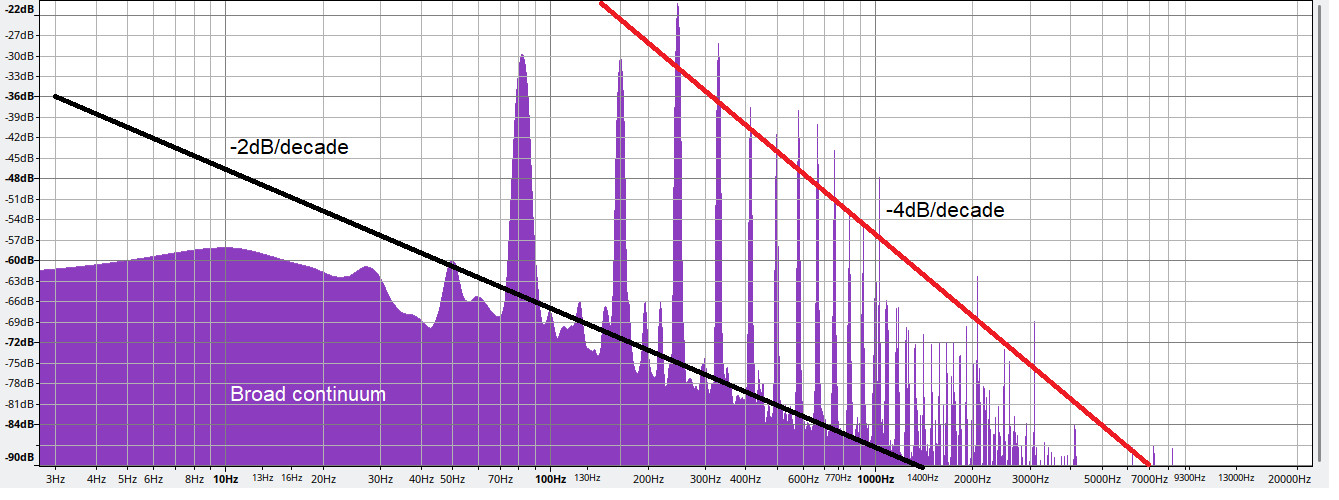enter image description here](Spectrogram of an acoustic guitar’s low E string showing broadened fundamental frequency and harmonic decay.)
As illustrated in the spectrogram above, the energy distribution across the spectrum acoustic guitar isn’t uniform. While an idealized model might predict harmonic amplitudes decreasing with the inverse square of frequency (and power with the inverse fourth power), the actual spectrum acoustic guitar shows deviations. The red line in the image approximates the expected decay of power with frequency to the fourth power. The noticeable deviation, especially for the fundamental and to a lesser extent the second harmonic, suggests that these lower frequencies lose amplitude and their spectral weight is distributed across a broader frequency range. The black line, decaying as the inverse square of frequency, indicates a curious trend in this spectral diffusion, though a definitive explanation for this behavior requires deeper investigation into the complex physics of string vibration and resonance within the spectrum acoustic guitar.
An interesting observation within the spectrum acoustic guitar is the potential for resonance between different strings. For instance, the third harmonic of the low E string (around 247 Hz) is close to the frequency of the open D string. The spectrogram shows a prominent third peak, which might be enhanced by the sympathetic resonance of the D string. Similarly, the fourth harmonic of the low E string could potentially resonate with the high E string. These inter-string resonances further contribute to the rich and complex character of the spectrum acoustic guitar‘s sound and its spectral representation.
In conclusion, analyzing the spectrum acoustic guitar reveals a fascinating departure from simple, idealized models of string vibration. The “washed out” fundamental, broadened harmonics, and complex energy distribution are all testament to the intricate interplay of string properties, resonance effects, and non-linear behavior within the instrument. Understanding these factors provides a deeper appreciation for the rich and nuanced sound of the acoustic guitar and the complex physics that underpins its musical voice.
