When you pluck a string on your guitar, you hear a note – but there’s a lot more happening in the sound than just that single pitch. A spectrogram, which visually represents the frequencies present in a sound, can reveal the complex “spectrum” of a guitar’s tone. You might expect a clear, strong peak at the fundamental frequency of a string, like the low E at roughly 82 Hz. However, analyzing a Guitar Spectrum often shows something more nuanced, sometimes even appearing as if the fundamental frequency is “washed out.” Let’s delve into why this happens and what it tells us about the rich sound of a guitar.
Guitar spectrum analysis showing the power distribution across frequencies. The red line illustrates the expected harmonic decay, while the black line shows the observed decay, highlighting the spread of the fundamental frequency.The idea of a perfect, isolated guitar string vibrating at a single frequency is a simplification we learn in basic physics. In reality, a guitar string, especially when part of a complete instrument, behaves far from this ideal. The “fundamental frequency” (like that 82 Hz for the low E) is indeed where the majority of the sound’s power originates, but the string’s behavior is influenced by many factors. These include how and where you pluck the string, the resonant properties of the guitar’s body and other strings, and even the intricate physical properties of the string itself.
Think of a guitar string not as a perfect, uniform spring, but as something with complex, non-linear characteristics. Its stiffness, for example, isn’t constant; it changes with frequency and how intensely the string vibrates. These non-linearities, along with the way the guitar body and other strings vibrate sympathetically, contribute significantly to the instrument’s unique “timbre” – the tonal color that makes a guitar sound like a guitar.
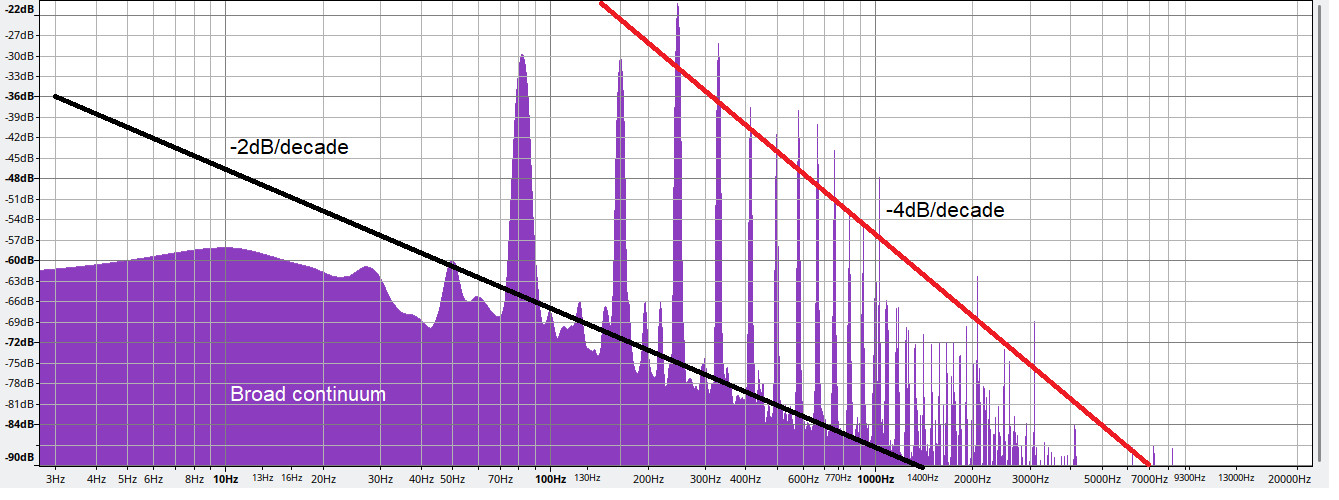
In an ideal scenario, a perfect string would produce sharp peaks in the spectrogram at multiples of the fundamental frequency – these are the harmonics. But in a real guitar spectrum, these peaks are broadened. This broadening, technically known as dispersion, is more pronounced at lower frequencies. This is why, in a spectrogram, the energy at the low-frequency end can appear spread out across a wider range, creating that “washed out” appearance of the fundamental. The higher harmonics tend to be less dispersed and appear more defined.
This dispersion arises because the speed of waves traveling along the guitar string isn’t constant across all frequencies. Lower frequencies, in particular, are more susceptible to these dispersive effects. This phenomenon, where wave speed depends on frequency, is not unique to guitar strings; it’s observed in various wave phenomena, as illustrated in this NPR clip discussing electromagnetic waves from lightning.
As pointed out in this Physics.SE answer, we’d anticipate the amplitude of harmonics to decrease inversely with the square of the frequency. Since power is related to the square of amplitude, it should diminish as the inverse fourth power of frequency. The red line in the spectrogram approximates this 1/frequency⁴ relationship. If guitar strings were perfect and resonance absent, the fundamental frequency’s peak would likely align with this red line. However, the spectrogram reveals that the fundamental and, to a lesser extent, the second harmonic, have lost amplitude, with their energy distributed across a broader low-frequency band. Interestingly, the black line indicates this energy spread seems to decay at a rate of roughly 1/frequency². While a definitive explanation for this specific decay pattern requires deeper analysis, it highlights the complex energy redistribution within the guitar spectrum.
One more thing to notice is that the third harmonic of the low E string (around 247 Hz) is close to the frequency of the open D string. Looking at the spectrogram, the third peak does seem prominent. It’s plausible that the D string is resonating, adding intensity to this third harmonic. Similarly, the fourth harmonic could resonate with the high E string.
Further insights into the complexities of guitar spectrograms and sound production can be found here.
In conclusion, the guitar spectrum is far more intricate than a simple series of fundamental and harmonics. The seemingly “washed out” fundamental frequency and the broadened spectrum at lower frequencies are not defects, but rather manifestations of the complex physics that give a guitar its rich, dynamic, and characteristically beautiful sound. Understanding these nuances allows us to appreciate the guitar not just as a musical instrument, but as a fascinating example of applied physics in acoustics.
